[Ɛ] es la quinta letra del alfabeto Griego. En la actualidad se utiliza para designar pequeñas cantidades que tienden a 0, como en los límites o también como la constante dieléctrica.
Salvar a Épsilon [Ɛ] es una gamificación transversal para el aula, tanto en la modalidad presencial como en modo híbrido, se encuadrada en la actividad "mejora tu cálculo", en el bloque de tareas relativas a operaciones aritméticas, para 4º y 5º de primaria, cuyo objetivo es el repaso de las restas con llevadas, trabajando las competencias matemática, social y digital.
Precisa de la colaboración activa del alumnado, para conseguir su objetivo final. Épsilon es nuestro nuevo compañero al que debemos ayudar. Se encuentra perdido en el interior de un laberinto y no sabe qué hacer. Cada vez que le ayudemos, resolviendo las pruebas, estará más cerca de encontrar la salida. ¿Queréis ayudarle?, eso si, se requieren para ello de grandes habilidades. Todo preparado y contamos contigo.
Descripción
Partimos con 10 ayudas, estas se irán consumiendo, una por cada día que pase sin obtener respuesta positiva de todos los participantes (salvo la primera vez que se considera de prueba). En ese caso Épsilon estará cada vez más perdido en el laberinto, ¿realmente queréis que esto ocurra?. No claro.
¿Cómo podemos ayudarle?, es fácil, deben responder correctamente cada alumno de la clase, un mínimo de 10 restas con llevadas, una etapa por día y según el recorrido elegido, podría requerir resolver entre 2 o 3 restas, por lo que al cabo 3 o 4 días y si todo va bien, [Ɛ] estaría salvado. Si queremos alargar el aprendizaje, podríamos bloquear algunos caminos, por lo que el alumno en cuestión deberá volver y elegir un nuevo recorrido. Cada mañana se debe presentar el estado de avance de [Ɛ], repasar con los alumnos los sucedido, el camino elegido por cada alumno, con las respuestas escritas, anotar los aciertos, cuantos errores se admiten, plantear la puntuación que debe alcanzar el grupo para salvar a [Ɛ] y así mantener vivo el interés en su salvación.
Las restas con llevadas deberán ser resueltas en casa, como ejercicio y enviadas como respuesta a la tarea de Google Classroom, en la que se pondrá cada etapa del día a realizar. Al termino del aprendizaje, se mostrará el laberinto resuelto, como un puzzle, compuesto por todos los caminos seguidos por los diferentes alumnos, se imprimirán y se pondrán en la pared del aula.
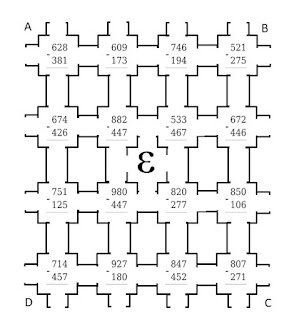
Supongamos el recorrido de Carolina, es una buena estudiante y ha resuelto perfectamente todas las restas del camino elegido, le hemos asignado el color amarillo. El primer día le aparece para realizar una nueva tarea. [Ɛ] se encuentra en el centro del laberinto.
Al día siguiente, vemos resuelto el primer recorrido,
Carolina lo ha hecho bien y tenemos el punto de salida al que ha llegado, lo
reconocemos gracias a las restas escritas que ha resuelto. Pero le vamos a
poner las cosas un poco mas difícil. Se encuentra con un obstáculo en su nueva
tarea, un incendio le obliga a retroceder. Debe por lo tanto ir a la tarea
anterior y elegir otro camino. Supone un extra de trabajo, pero no debe
desanimarla.
Carolina corrige y sale por la salida inmediata inferior,
lo que le permite atravesar la segunda etapa del tirón. Ha tenido que realizar
una resta extra, pero con cuatro mas se encuentra en la siguiente etapa.
Carolina lleva hechas siete restas hasta el momento. Se
podría ampliar a una o dos etapas mas, para alcanzar las 10 restas con llevada
mínimas previstas. Al final podemos componer un pequeño mosaico (o grande,
según el número de alumnos), con todos los caminos seguidos por el grupo.
Recuerda referenciar las caras de las etapas, de esta forma podremos construir
el mosaico con facilidad.
Este podría ser el resultado final para Carolina, imaginaos
como podría quedar para la totalidad del alumnado.
Por último, para llevar el control de la gamificación hemos
creado el seguimiento en Excel. En este se pondrán fijar las
condiciones y podremos empezar.
Elementos TIC utilizados en este artículo.
OneNote - Preparación esquema y contenidos.
PowerPoint - Plantilla y creación de los diferentes etapas.
Adobe Acrobat DC - Para la manipulación de PDF's.
PS Express - Para recortes de imágenes y composiciones.
SketchBook - Para composición del lienzo final.
Stop Motion - GIF animados.
Excel - Seguimiento de la puntuación.
Paint - Convertir gráfico Excel en imagen.
Para su Integración en Blogger de Google.
Fuente consultada.